8691. Крупногабаритный флиппер для блинов

В прошлом году Бесконечный Дом Блинчиков представил новый вид блинов. Блин имеет счастливое лицо из шоколадной стружки с одной стороны (“счастливая сторона”) и ничего с другой стороны (“пустая сторона”).

Сегодня Вы главный дежурный повар. Блины готовятся в один ряд на горячей поверхности. В рамках своих бесконечных усилий по максимизации эффективности, Дом Блинчиков недавно предоставил Вам крупногабаритный флиппер для блинов, который переворачивает ровно k последовательных блинов. То есть для последовательно расположенных k блинов он заменяет каждый блин счастливой стороны блином пустой стороны, и наоборот. При этом порядок блинов слева направо не меняется.

Вы не можете переворачивать с помощью флиппера менее k блинов за раз, даже на конце ряда (поскольку на обеих сторонах варочной поверхности имеются выпуклые края). Например, вы можете перевернуть первые k блинов, но не первые k – 1 блинов.

Ваш ученик-повар, который все еще изучает работу, просто использовал старомодный флиппер для одного блинчика, чтобы перевернуть несколько отдельных блинов, а затем побежал с ним в туалет, как раз перед тем, как клиенты начали приходить на кухню. У Вас остался только негабаритный флиппер для блинов. Вам нужно быстро его использовать, чтобы все блины были перевернуты счастливой стороной. Тогда клиенты останутся довольны своим визитом.

По заданному состоянию блинов подсчитайте минимальное количество использований негабаритного флиппера для блинов, необходимых для переворачивания всех блинов счастливой стороной вверх, или укажите, что сделать это невозможно.

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 100). Далее следуют t тестов. Каждый тест содержит одну строку s и целое число k (2 ≤ k ≤ длина s). s задает строку блинов: каждый символ равен или + (блин лежит счастливой стороной вверх) или - (блин лежит пустой стороной вверх).

Выход. Для каждого теста вывести строку содержащую Case #x: y, где x номер теста (начиная с 1) и y либо IMPOSSIBLE если невозможно перевернуть все блины счастливой стороной вверх, либо число – наименьшее количество раз применения флиппера для достижения цели.

Пример входа	Пример выхода
3 ---+-++- 3 +++++ 4 -+-+- 4	Case #1: 3 Case #2: 0 Case #3: IMPOSSIBLE

РЕШЕНИЕ

жадность

Анализ алгоритма

Заметим, что использование флиппера коммутативно. То есть при выполнении набора переворачиваний блинов в любом порядке получается один и тот же результат. Применять флиппер более одного раза в одной и той же позиции нет смысла – два применения флиппера не изменяют положеня блинов.

Пусть строка s = s₁s₂ … s_n задает положение блинов. Обозначим через f_i применение флиппера в позициях s_i s_i+1 … s_i+k-1.

Если s₁ = ‘-‘, то сменить эту позицию на ‘+’ можно только совершив операцию f₁. После того как станет s₁ = ‘+‘, дальше смотрим на s₂. Если s₂ = ‘-‘, то следует совершить операцию f₂ и так далее. Получаем жадную идею решения задачи. Максимальной позицией, на которой можно применить флиппер, будет n – k + 1. В этом случае блины будут перевернуты в последних k позициях: s_n-k+1 s_n-k+2 … s_n. После того как блины во всех позициях от 1 до n – k + 1 будут лежать счастливой стороной ввверх, следует проверить, что на последних k – 1 позициях они также расположены счастливой стороной ввверх. Если это не так, то требуемое расположение блинов невозможно.

Пример

Рассмотрим первый пример. Ширина флиппера k = 3. Начальное расположение блинов следующее:

1. s[1] = ‘-‘, применяем операцию f₁.

2. s[5] = ‘-‘, применяем операцию f₅.

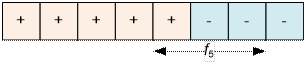
3. s[6] = ‘-‘, применяем операцию f₆.

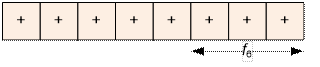
Позиции 7 и 8 содержат ‘+’, так что цель достигнута в результате трех применений флиппера.

Реализация алгоритма

Функция flip реализует операцию f_pos – применение флиппера в позициях s_pos s_pos+1 … s_pos+k-1.

void flip(int pos)

{

for (int i = pos; i < pos + k; i++)

if (s[i] == '+') s[i] = '-'; else s[i] = '+';

}

Основная часть программы. Читаем входные данные.

cin >> tests;

for (i = 1; i <= tests; i++)

{

cin >> s >> k;

В переменной cnt подсчитываем количество применений флиппера.

cnt = 0;

Двигаемся по позициям слева направо, начиная с нулевой. Если s[j] = ‘-‘, то применяем операцию f_j.

for (j = 0; j <= s.size() - k; j++)

if (s[j] == '-')

{

flip(j); cnt++;

}

На последних k – 1 позициях блины должны находиться счастливой стороной вверх (‘+’). Если это не так, то установим flag = 1 и ответ будет IMPOSSIBLE.

flag = 0;

for (j = s.size() - k + 1; j < s.size(); j++)

if (s[j] == '-') flag = 1;

Выводим ответ.

cout << "Case #" << i << ": ";

if (flag == 1) cout << "IMPOSSIBLE" << endl;

else cout << cnt << endl;

}